
|
|
Abstract: How ideas drawn from the study of chaos theory can be used to describe some aspects of a social environment. Notes: Presented at the Annual Meeting of the Canadian Sociology and Anthropology Association, University of Calgary, June 1994. Updated 1997. |
Chaos as Metaphor for the Study of Social Processes in the Postmodern World:
A Baha'i Illustration
by Will C. van den Hoonaard and William W. Hackborn
1997-03Acknowledgements: We are grateful to Dr. Scott Grills of Augustana University College, Dr. Patrick Baker of Mount Allison University, Dr. Margit Warburg of Copenhagen University, and Dr. Noel Iverson of the University of New Brunswick for commenting on an early draft of this paper.
Abstract: This paper shows how ideas drawn from the study of nonlinear dynamical systems, popularly known as chaos theory, can be used to describe some aspects of a social environment. We have chosen three features which appear frequently in contemporary Bahá'í communities and which are central to the Bahá'í view of the postmodern social world: fragmentation, diversity, and unity in diversity. For each of these features, we have chosen a dynamical system that illustrates it in a metaphorical, highly qualitative way. The dynamical systems we have selected are caricatures, metaphors for these features; they are not intended to be models in any quantitative sense. Our second objective is to present some of the fundamentals of chaos theory in a way that will be interesting and useful to social scientists.
Our primary objective is to show how ideas drawn from the study of nonlinear dynamical systems,[1] popularly known as chaos theory, can be used to describe some aspects of a social environment. We have chosen three features which appear frequently in contemporary Bahá'í communities and which are central to the Bahá'í view of the postmodern social world: fragmentation, diversity, and unity in diversity. For each of these features, we have chosen a dynamical system that illustrates it in a metaphorical, highly qualitative way. The dynamical systems we have selected are caricatures, metaphors for these features; they are not intended to be models in any quantitative sense.[2]
Our second objective is to present some of the fundamentals of chaos theory in a way that will be interesting and useful to social scientists. The descriptions of our dynamical systems require of the reader a modest level of mathematical sophistication, but they include all the concepts necessary for a non-superficial understanding of the systems.
Bahá'ís are members of a world-wide movement, which presently numbers between 5 and 6 million, and which is regarded as "almost certainly the largest and fastest growing of the [new religious movements] (MacEoin, 1986: 1).[3] It is a movement with progressive social teachings on human rights, the equality of men and women, world peace, world order, and global prosperity, while maintaining a strict moral code of personal behavior. The movement, founded by Bahá'u'lláh (1817-1892), originated in mid-19th-century Persia, but grew steadily beyond the borders of Persia, especially to North America and Europe since just before the turn of the century. During World War II, the Bahá'í Faith[4] began systematically to spread to Latin America. From the 1950s onwards, Bahá'í communities could be found in Africa and Asia, in which the Bahá'í Faith emerged as primarily a "Third-World religion" (MacEoin, 1986: 1). One of the most recent dramatic demographic changes in the Bahá'í world community involves the resettlement of thousands of Iranian Bahá'ís, refugees from persecution in Iran. The process of integration of these Iranian Bahá'ís in Western countries, and in Canada in particular, is the subject of our paper.
What gives added focus to our study are the Bahá'í teachings, with their ideological stress on unity in diversity. These teachings, Bahá'ís believe, speak to the contemporary human condition and delve substantially into the nature of human fragmentation and diversity. The infusion of Iranian Bahá'ís into Western society provides us with an opportunity to see how these ideological concerns play themselves out in Canadian Bahá'í communities. Chaos theory provides insights into the social processes that attend Bahá'í communities undergoing these demographic and cultural changes.
The Appropriateness in Using Socialization as a Model in this Study
As our study focuses on the relations of two Bahá'í groups (namely, the host Canadian Bahá'ís and newly arrived Iranian Bahá'ís),[5] some would think it appropriate to analyze these relations in terms of the processes of socialization which allow one group to be assimilated by the receiving group. We argue that such an approach is inadequate to our task. We base our assessment on both methodological and epistemological grounds.
Ever since Dennis Wrong's article (1961) alerting us to the "oversocialized" conception of humans, sociologists have been more circumspect in the use of the term socialization. As many contemporary introductory textbooks in sociology indicate, sociologists are more likely to discuss socialization in terms of individual or personal relations, rather than as a defining social process among social groups. Much of the recent literature on ethnic relations, for example, has gone beyond defining ethnic relations in terms of a simple, unidirectional relationship involving assimilation or socialization. The concept "socialization" fails to recognize the complex relationships that individuals, sets of individuals, and subgroups use in dealing with each other.
Beyond its failure to account for complex inter-group relations, the use of "socialization" as a conceptual tool is also limited in other ways: the groups in our study cannot be defined in terms of dominant/subordinate relations which would invoke either socialization or assimilation. Four studies on the relationship between newly arrived Iranian Bahá'ís and Bahá'ís in a host society (Denmark, Italy, Australia, and Los Angeles) support our argument that the relations between Iranian and host Bahá'ís are more likely to express structural equality, rather than assimilative relations.
Warburg (forthcoming: 23), for example, in her study of the Danish Bahá'í Community suggests that "the Iranians possessed knowledge, insight and experience of the religion at a level hitherto unknown in the Danish Bahá'í Community." While the Danish Bahá'ís have arrived in the Bahá'í community mostly through conversion, consist primarily of women, and see themselves as members of a minority religion that does not exist in a hostile environment, the Iranian Bahá'ís have come to their religion through their families, exhibit equal sex ratios, and see themselves as having lived in a very hostile society (i.e. Iran). Perhaps most importantly, the Danish Bahá'ís regard the Iranian Bahá'ís with very high regard and have high expectations of them (Warburg, forthcoming).
Chantal Saint-Blancat in her study of Iranian immigrants in Italy (1989:32) concluded that the immigrant Iranian Bahá'ís do not see themselves as "Iranians," but more as Bahá'ís devoted to a Bahá'í world order; "nationality" plays a very minor role, if at all. Italian Bahá'ís are more likely to see Iranian Bahá'ís as co-religionists. The Iranian Bahá'ís, according to Saint-Blancat, see themselves as world citizens. Such attitudes are the key by which Iranian Bahá'ís insert themselves into Italian society, where more than 70% of the Iranian Bahá'ís identify themselves as Italians (Saint-Blancat, 1989: 34). Significantly, there are also more pronounced differences between Iranian Bahá'ís and other Iranians than between Iranian Bahá'ís and Italian Bahá'ís (Saint-Blancat, 1989).
A third study offers a similar finding: Feather et al. (1992: 104) found that there were many observed similarities between the 124 Australian and Iranian Bahá'ís who endorsed the values permeating their common religion; only in some of the cultural characteristics were there differences related to individualistic and collectivist interests. There were more pronounced differences between men and women (Feather, 1992: 104) than between Australians and Iranians.
Bozorgmehr's study (1992: 245) of Iranians in Los Angeles, United States, confirm the findings of the above-mentioned research: Iranian Bahá'ís, compared to other Iranians (Jews, Muslims, and Armenians), have wider social networks with respect to the inclusion of non-Iranians.
Thus, the assimilation/socialization model that can define the relationship between two groups is an inappropriate one for our study. Hence, we desire to see the relationship between the hosts and Iranian Bahá'ís as a structural issue. Thus, one cannot elucidate the changing character of Bahá'í communities by merely casting their change in unidirectional terms, but must conceive the change in another way: deeply imbedded changing social structures that mark the post-industrial age, within Bahá'í communities and the society at large. What we need is a theory that advocates the nonlinear nature of such change, namely chaos theory. When such a theory is matched with the ideological underpinnings of the human phenomenon under study (which has explicit ideas about social fragmentation, diversity, and unity in diversity), we may arrive at insights not otherwise accessible.
The Study of Nonlinear Dynamical Systems
The study of nonlinear dynamical systems has, in the last twenty years, initiated something of a paradigm shift in the natural sciences. In physics, researchers have found that even systems described by classical Newtonian theory can exhibit chaotic dynamics.[6] In chemistry and biology, scientists have used chaos theory to analyse certain reactions and natural processes.[7] We use the phrase chaotic dynamics to designate all of the diverse and often unpredictable behavior associated with nonlinear dynamical systems. We define a dynamical system to be a set of deterministic mathematical equations that describe how certain variables evolve in time. Such a system is termed nonlinear if the current and former values of its variables are related in a non-proportional way; this kind of relationship is sometimes labelled nonlinear feedback.
The dynamical systems used to model natural phenomena are often nonlinear, a fact that generally makes the solutions to such systems difficult to analyse. The term chaos[8] was coined to suggest the surprisingly complicated and, at times, apparently random behavior observed in numerous nonlinear dynamical systems. However, it is important to realize that chaotic dynamics may also involve striking patterns, coherence, and order.[9]
Social scientists have only very recently considered the implications of chaos theory for their various fields of study. The writings of Baker (1993), Young (1991a, 1991b), and Gregersen and Sailer (1993) come to mind as notable explorations of those implications.
Baker (1993) traces the intellectual and social contexts which gave rise to chaos theory and argues that the theory is of particular use in the analysis of societal evolution, involving social forces between the weak periphery and the strong centre (Baker, 1993: 140-1). Their interaction is characterized by mutually affecting strategies, leading to turbulence. The turbulence is caused by the greater effort and energy required to effect increasingly complex strategies.
Young (1991a, 1991b) asserts that chaos theory challenges many of modern science's cherished ideals: predictability, causality, formal deductive models, reductionism, and generalization. He argues that chaos theory affirms what many social scientists have argued for the better part of this century, namely that "the mission of social science changes from a quest for a stable codification of social laws to a more intersubjective and political endeavor in which human choice is used to shape and to elicit the knowledge process" (Young 1991a:328). Young also describes many of the important entities in chaos theory (such as attractors, bifurcations, and fractals) and their significance for social researchers.[10] One of the articles (1991a), moreover, attempts to correlate chaos theory and symbolic interaction theory, while the other (1991b) goes into more detail concerning the role of chaos theory in understanding social change.
Gregersen and Sailer (1993) are more specific when they suggest that qualitative methods provide the means to identify and work with chaotic systems, so common in social dynamics. They further argue that social scientists so rarely discuss chaotic systems because they are difficult to identify or work with.
We agree with the general conclusions of all four authors, but wish to use chaos theory to deepen our understanding of what we consider to be the salient features of the postmodern world.[11] It could be argued that chaos theory merely shows that natural scientists are beginning to come to terms with the world views of social scientists. However, we feel that chaos theory offers the latter group an opportunity for dialogue with the former and a new perspective on social phenomena.
Fragmentation, Diversity and Unity in Human Culture.
A synoptic view of contemporary society--the postmodern world--hardly does justice to its immense social transformation. Some authors describe it as a post-industrial society (Touraine, 1974), the "second great divide in human history" (Toffler, 1970). Postmodernists (e.g. Harvey, 1989; Smart, 1993) place importance on the fragmentary character of our society, while others (e.g. Barber, 1992) emphasize the trend of globalization, and regional unification in some spheres of human life. Our attention is drawn to these trends, namely the processes of fragmentation, diversification, and unification. Some, like Baker (1994), aver that these processes may indeed be the "harbingers of a new more complex unity."
Metaphors from chaos theory allow us to visualize all of these processes. Specifically, in examining social fragmentation, we are using the pitchfork bifurcation equation, while a discrete dynamical system is used to illustrate social diversity. The Lorenz system provides a metaphor for unity in diversity.[12]
A Metaphor for Social Fragmentation
The fragmentation of prevailing social structures (e.g., communities, moral systems) is one of the distinctive features of our time (Shoghi Effendi, 1974: 188-191). In the pre-fragmentary period, fundamental assumptions and the prevailing ideological paradigm are not questioned. Metaphorically speaking, we can compare the period that inaugurates fragmentation to a pitchfork, when the social order bifurcates into alternative streams. In such times, ideological fence-sitting is no longer an option and fundamental assumptions are questioned.
The pitchfork bifurcation equation[13] provides a good metaphor for this process. This equation has a variable, x, and a parameter, p. In a typical application, p is held constant at some arbitrary value, but x is given some initial (i.e., at time zero) value and then evolves continuously as time advances in accordance with the equation. If p is less than or equal to zero, x evolves toward the value zero no matter what its initial value is; in this case, the value x = 0 (i.e., a value of zero for x) is termed an attractor and is said to be stable. However, if p is greater than zero, x evolves toward the value ?p (i.e., the square root of p) if the initial value of x is greater than zero, and toward the value -?p if the initial value of x is less than zero; in this case, the values x = ?p and x = -?p are attractors, and the value x = 0 is a repeller and is unstable. The values x = 0, x = ?p, and x = -?p (for p greater than zero) are also called fixed points since if x is initialized to one of these values, it will remain at that value for all future times.[14] A bifurcation[15] is said to occur at the value p = 0 since, at this value, the attractor x = 0 splits, in a sense, into the two attractors x = ?p and x = -?p.
The dynamics of the pitchfork bifurcation can be displayed graphically using a
Cartesian grid on which p is plotted on the horizontal axis and x on the
vertical axis. This has been done in figure 1.
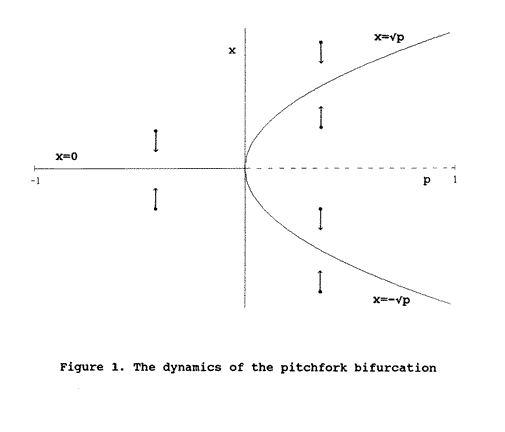
In this figure, the value x = 0 (coinciding with the p-axis) is denoted by a solid line where it is stable (i.e., for p less than or equal to zero) and as a dashed line where it is unstable (i.e., for p greater than zero). The attractors x = ?p and x = -?p are denoted by solid curves.[16] The dotted line designates the x-axis (on which p = 0). Points and arrows are used to indicate typical initial values of x and the resulting directions in which x varies. Since x is the only variable in the pitchfork bifurcation equation, the phase space, the set of all possible values of x, is said to be one-dimensional. Each vertical slice of figure 1 represents a copy of the phase space in which the behavior of the variable x for a particular value of the parameter p is depicted.
Now, let us use the pitchfork bifurcation as a metaphor for the fragmentation of a community due to ethnic and cultural forces. Assume that the parameter p is a measure of the ethnic diversity of the community: suppose the value p = -1 denotes a state of total ethnic homogeneity in the community, the value p = 1 denotes a state of total ethnic heterogeneity, and values of p between -1 and 1 form a continuum of possible states between these two extremes. When the ethnic composition of the community is largely homogeneous, we expect there to be a cultural mainstream to which individuals in the community, even those few from minority ethnic groups, feel attracted (Cf., Blau, 1977).[17] We use the variable x in the pitchfork bifurcation equation to represent a kind of social-psychological distance between an individual in the community and this cultural mainstream, designated by the fixed point x = 0.
Within our metaphor, the parameter value p = 0 represents a critical level of ethnic heterogeneity with respect to the stability of the cultural mainstream. When p is less than or equal to zero, the cultural mainstream is an attractor. However, when p exceeds zero, this cultural mainstream becomes a repeller and is replaced by two other attractors. There are many new attractors that one could imagine, but we wish to elaborate on two attractors that are particularly important from a Bahá'í perspective: the first of these (which we will associate with the attractor x = ?p in the pitchfork bifurcation) represents a cultural fusion to which each of the different ethnic cultures contributes and in which there is an emphasis on the harmony and solidarity of the community; the second attractor (which we will associate with the value x = -?p) represents a kind of fundamentalism in which other ethnic cultures in the community are viewed as alien and subversive.
The former attractor will be termed altercentricity[18], and the latter, ethnocentricity. It should be borne in mind that these attractors represent extreme positions to which individuals are drawn over time but which may not ever actually be reached. People who totally accept, or totally reject, cultures other than their own are rare. Within our metaphor, people are simply moving one way or the other, and the fragmentation of the community results from the fact that not everyone is moving in the same direction.[19] Of course, in any given community in which this sort of fragmentation is occurring, factors ignored in our metaphor will influence the rate at which fragmentation develops and the proportion of those who are drawn towards one or the other of the attractors.[20]
It may not be clear how the cultural mainstream, an attractor in sufficiently homogeneous conditions, becomes unstable when the ethnic diversity of the community exceeds a critical level. It could be argued that, since some individuals would continue to be drawn to this cultural mainstream, it remains one attractor (among others) even in highly heterogeneous situations. However, we contend that this cultural mainstream involves an essential ignorance about, and therefore a neutrality towards, minority cultures. When the community becomes sufficiently heterogeneous, this kind of neutrality is no longer possible: people either begin to include their neighbours' cultures, or they exclude them by deliberate action or by inaction. Hence, we would argue that those who continue to support the cultural mainstream are actually moving towards the ethnocentricity attractor since they are, to some extent, reacting against the ethnic diversity of their community. Those who aggressively promote their own ethnic culture, at the expense of other cultures including the former mainstream, are also moving towards the ethnocentricity attractor.
In recent years, Bahá'í communities in urban Canada have made such a dramatic shift in their ethnic makeup that a critical juncture has been reached in many cases. Since 1980, more than 2,000 Persian Bahá'ís arrived in Canada on account of the wave of on-going religious persecution in Iran. Within a few years, there was one refugee Iranian Bahá'í for every 30 Canadian Bahá'ís (Bahá'í Canada, Sept-Oct. 1982: 34). Attractors play a particularly important role in these local urban Bahá'í communities where distinctively different behavior patterns are emerging.
It should be noted, at the outset, that Persian Bahá'ís have not set up their own residentially-segregated communities, as they have settled in areas already populated by Canadian Bahá'ís. Because large urban centers, such as Montreal, Toronto, and Vancouver, have tended to attract the majority of Persian Bahá'ís, Bahá'í communities in these centers have become Persianized. A similar process has occurred in the Bahá'í communities of smaller cities which experienced a relatively large influx of Persians.[21]
Persian Bahá'í culture involves the use of the Persian language in social and administrative settings (Anon., 1988: 5). It affects particular religious habits (see, e.g. Howe, 1988: 3; Rafat, 1988: 16) and cultural practices (Danesh, Nov. 1986: 6; Rafat, 1988: 16; Feather et al, 1992) considered to be different from those practised by Canadian Bahá'ís. Marriage and family customs (Rafat, 1988: 16) are at variance as well. Some Bahá'í-related practices (MacEoin, 1989; Rafat, 1988: 16), organizational attitudes (Danesh, 1988: 16; Rafat, 1988: 16), and the universe of discourse[22] also appear to differ from Canadians. One study (Anon., 1988) of the Waterloo, Ontario, Bahá'í community reported that "the general level of integration between the two groups is fairly low."
This Persianization of Bahá'í communities in urban Canada has created a marvellous opportunity for examining communities with various levels of ethnic diversity (i.e., with various values of the parameter p used in the pitchfork bifurcation equation). In many cases, Persianization has destabilized the home-grown, Canadian, cultural mainstream and replaced it with the altercentricity and ethnocentricity attractors discussed above.[23] In this kind of fragmentation, occurring during the earliest phase of integration of the communities, altercentricity is demonstrated by such things as a willingness to incorporate the practices of both Persian and Canadian Bahá'ís in communal worship, and by efforts to overcome the language barrier in order to develop deeper relational bonds within the community. On the other hand, ethnocentricity sometimes manifests itself as condescension, intolerance (Rafat, 1988: 16), or an insistence that procedures be done in certain ways.
The tension between altercentricity and ethnocentricity is sometimes quite evident in urban Canadian Bahá'í communities. For example, Bahá'ís have nine religious holy days throughout the year, and they are encouraged to observe[24] these holy days, partly in order to foster a shared community experience. Generally, Persian Bahá'ís are far more accustomed to celebrating these holy days than Canadian Bahá'ís. Sometimes altercentric Bahá'ís encourage the observation of these holy days so zealously that they discourage, implicitly or explicitly, the celebration of traditional Canadian festivals such as Christmas and Easter. This generates some alienation among Bahá'ís who are closely tied to Canadian cultural traditions.
It is quite remarkable that, in a fragmentation process described by the pitchfork bifurcation equation, a small change in an individual's attitude (represented by a small change from a small negative x value to a small positive one, or vice versa) has far-reaching consequences in terms of the attractor to which that individual is drawn (Warburg, 1993). With respect to fragmentation in Canadian Bahá'í communities, the Bahá'í writings, which consistently favor altercentricity over ethnocentricity, often encourage the small attitudinal changes that will enable individuals to move towards the former attractor in lieu of the latter. It must be noted, however, that efforts such as these are external to our pitchfork bifurcation metaphor, and the impact of such efforts may be unpredictable due to the nature of nonlinear dynamics.
A Metaphor for Social Diversity
In the pitchfork bifurcation described above, a straight line (x = 0) separates the initial values (of the variable x) associated with solutions that evolve toward one or the other of the two attractors emerging from the bifurcation. However, in higher-dimensional nonlinear dynamical systems, it is usually very difficult to predict which initial conditions are associated with solutions that are drawn to a particular attractor. We have chosen a discrete dynamical system[25] (also called a mapping) to illustrate this idea; it will be seen below that this dynamical system can also be regarded as a metaphor for social diversity.
In a discrete dynamical system, time and the associated variable(s) vary in
discrete steps (unlike the pitchfork bifurcation equation in which the variable
varies continuously with time). In our example, the system has two variables,
x and y, which will be written as a point (x,y). The system has three fixed
point attractors corresponding to the three (complex number) cube roots of the
number one: (1,0), (-½,½?3), and (-½,-½?3). As time advances, the solution
associated with almost any initial values of x and y will eventually converge
to one of these attractors, though it may first wander widely for many
iterations. An attractor's basin of attraction is the set of all
initial values associated with solutions that converge to that attractor.
Figure 2 depicts the two-dimensional phase space for our chosen dynamical
system on a Cartesian grid with x and y plotted on the horizontal and vertical
axes respectively. The symbol "+" in this figure indicates the fixed point
(1,0), and the white region represents its basin of attraction. (The basins of
attraction of the other two fixed point attractors may be obtained by rotating
the white region by 120 and 240 degrees; hence, the three basins of attraction
are congruent.)

The basin of attraction shown in figure 2 is almost unimaginably complicated; in fact, its boundary is said to be a fractal since it can be regarded as having a fractional dimension lying between one and two (Becker and Dörfler, 1989:103). In the vicinity of this boundary, two solutions associated with two nearby initial points may be drawn to different attractors. This phenomenon, known as sensitive dependence on initial conditions, makes prediction of the eventual outcome of a solution notoriously difficult. We will examine how this phenomenon can be reflected in a Bahá'í community.
Diversity is an important concept in the Bahá'í Faith. The Bahá'í writings urge the recognition and respect of human and cultural diversity.[26] Bahá'ís, as a whole, comprise a body of people from virtually every country and ethnic group on the planet (Hatcher and Martin, 1985:168). The nonlinear dynamics depicted in figure 2 seems, to us, to be a fitting metaphor for some aspects of a Bahá'í community's potential diversity.
To illustrate, imagine that the points of figure 2 correspond to the members of a large, diverse, local Bahá'í community. Now, consider, for example, three issues about which Bahá'ís generally care deeply: say, racial harmony, gender equality, and international cooperation. If each Bahá'í in the community were asked to name which of these issues attracts more of her or his attention, the set of those who name a particular issue would likely have some of the fractal characteristics of the basin of attraction in figure 2. This metaphor reflects the potential diversity of a Bahá'í community in two ways: first, the three different attractors suggest the diversity of hopes and concerns of community members; secondly, the infinity of points in phase space, with their independent behavior possibly so different from that of their neighbors, suggests the limitless human diversity (and unpredictability) of the individuals within the community.
Of course, figure 2 offers only a very fanciful metaphor for any process involving real, human, social dynamics. However, we wish to stress that a complex social system (which will almost certainly involve nonlinear processes) can be expected to possess intricate dynamics which, in a loose, qualitative way, are similar to those portrayed in figure 2. Dynamics of this kind defy easy classification and prediction. Young coins the phrase "fractal causality" (1991a:328, 1991b:293) to refer to the weakened notion of cause and effect that is implied by these dynamics.
A Metaphor for Unity in Diversity
The unity of humankind is the fundamental theme of the Bahá'í Faith.[27] However, the unity sought by the Bahá'í teachings is not one that suppresses cultural singularity. Rather, it is a unity that, while encouraging group identity at various levels, advocates a wider allegiance to humanity as a whole. Bahá'ís often use the phrase unity in diversity[28] to describe this apparently paradoxical concept; we will abbreviate this phrase to unidiversity. Unidiversity is an ideal for which Bahá'ís are encouraged to strive, but even within the Bahá'í community, it has by no means been attained, and it is not clear what form this ideal might eventually take. It could be argued that such an ideal "would never be attained in the sense that it would be coevolutionary and dynamic" (Baker, 1994). Most Bahá'ís would concur, however, that unidiversity will entail an unprecedented level of human cooperation, interaction, and organization. The Lorenz system[29] provides an exquisite metaphor for this still unfolding notion of unidiversity.
The Lorenz system involves three variables, written here as a point (x,y,z),
which vary continuously with time, and (in our treatment) one parameter R. For
different values of R, the Lorenz system shows both of the behaviors mentioned
in the last two sections. When R equals one, the system undergoes a
three-dimensional pitchfork bifurcation in which the fixed point (0,0,0), which
is the only attractor for values of R less than one, becomes unstable and two
new fixed point attractors emerge from it. As R is increased through values
greater than one, these two fixed point attractors become less and less stable,
and solutions may wander almost randomly for some time before finally
spiralling toward one of them. Eventually, when R is about 24.74, the two
(former) attractors become unstable and solutions begin to spiral away from
them. Figure 3 shows a typical solution in phase space[30] with R equal to 28.
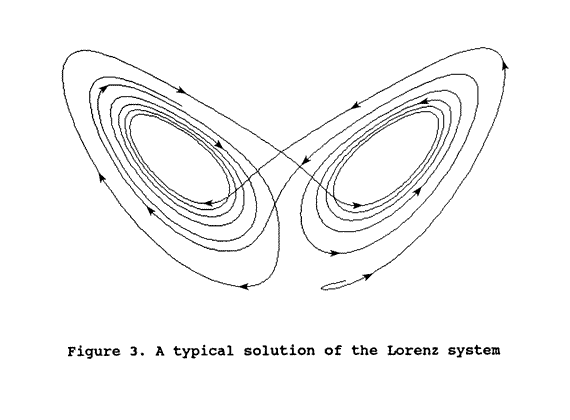
The arrows on the solution in figure 3 indicate the direction in which the variables (x,y,z) of the solution evolve as time advances; the outward spiralling of the solution from two fixed points as time proceeds is apparent from these arrows. The solution continually spirals away from a fixed point until the spiral becomes sufficiently large, at which point the solution jumps to a position closer to the other fixed point and an outward spiral begins again. It may seem that the solution depicted in figure 3 is converging to no attractor, but, in fact, it is converging to an object known as the Lorenz attractor. Mathematicians conjecture (though it has yet to be rigorously proven) that the Lorenz attractor is a fractal whose dimension is between two and three, and that a solution lying on the Lorenz attractor never returns to a previous state but eternally explores new points on the attractor; the Lorenz attractor is an example of a mathematical entity called a strange attractor. The striking pattern and order inherent in the complicated dynamics of the Lorenz attractor are clearly revealed by the phase space portrayal in figure 3. (Other ways of portraying solutions of the Lorenz system, such as time series, do not expose this pattern.) However, sensitive dependence on initial conditions, an almost ubiquitous feature of chaotic dynamics, is also an attribute of the Lorenz attractor: two solutions with nearly identical initial points on the attractor soon diverge and wander independently, often on different spirals. The Lorenz attractor embodies, in a sense, a seething chaos within a high level of order and organization.
The Lorenz attractor is also an elegant representation of the concept of unidiversity. To illustrate, imagine that the points of phase space represent the whole variety of human cultures that are theoretically possible. Since any solution of the Lorenz system, no matter what its initial point, is drawn to the Lorenz attractor as time advances, the Lorenz attractor, within this metaphor, represents a convergence of human cultures into something of a common culture, a kind of unity of cultures. However, this unity of cultures is infinitely more diverse than the cultural uniformity represented by a fixed point attractor. Moreover, the two unstable fixed points, around which solutions spiral outwardly in the Lorenz attractor, can be thought of as symbols for one's own local culture and the local cultures of others. When unidiversity is practised, one's individual awareness, symbolized by a solution of the Lorenz system, naturally centers at times on one's own local culture, but the local cultures of others are inevitably the center of one's awareness at other times.
This decentering and recentering of individual awareness seems to attend the collective life of developing Bahá'í communities in small Canadian towns. When Persian Bahá'ís have settled in such towns,[31] there is a far greater tendency for these communities not only to retain their Western character, but also to adopt elements of Persian culture. Under these circumstances, there is an intensified awareness of diversity. Not only do we find varying degrees of awareness of one's own background, but also of an awareness of Persian culture. Given the small social and physical space of Bahá'í communities in such towns, there appears to be a cultivated awareness of a future Bahá'í culture. These multiple awarenesses wax and wane in relation to the contingencies of everyday life. Turbulence indeed!
The way the dynamics of the Lorenz system change as the parameter R slowly increases, where R starts at a value less than one, is sometimes termed the Lorenz route to chaos.[32] This route, which describes an evolution of sorts, is somewhat analogous to the way Bahá'ís view the evolution of an initially isolated human community as its interaction with other communities gradually expands: an initial stage of social uniformity (analogous to a single fixed point attractor) experiences a bifurcation wherein it is replaced by a contentious diversity (analogous to a pair of competing fixed point attractors) which, in turn, is eventually replaced by unity in diversity (analogous to the Lorenz attractor). Just as the Lorenz attractor emerges in the evolution of the Lorenz system, unidiversity is envisioned by Bahá'ís as something that will emerge in the evolution of human communities. Furthermore, within our evolutionary metaphor, the fragmentation that produces altercentricity and ethnocentricity is simply a phase encountered on the path to unidiversity.
Young's concept of ultrastability, which he associates with "our contradictory desire for freedom and community" (1991b:297), is somewhat similar to our concept of unidiversity. In fact, Young states that the "attractor of Lorenz would exhibit ultrastability" (1991b:305). Young, however, uses the Mandelbrot set,[33] an intricate planar region with a fractal boundary, as his principal image of ultrastability.
Baker (1993) coined the term centriphery to capture the dynamics that underlie the social interactions of a society's center and its periphery. In his view, centriphery is an attractor which "creates the turbulence and recreates the order in social life" (Baker, 1993:135). Baker's centriphery, while it is similar to unidiversity, resembles more closely our notion of altercentricity since both centriphery and altercentricity have a single center, whereas unidiversity, symbolized by the Lorenz attractor, has two centers corresponding to two unstable fixed points. This is consistent with Baker's remark that humans' "centering and peripheralizing activities compete with the centering and peripheralizing activities of others, for others are similarly trying to center their worlds" (Baker, 1993:139).
There are some fascinating correlations among the Lorenz route to chaos and the concepts of energy and complexity in physical and social systems. Physically, the parameter R in the Lorenz system measures the amount of energy that a convection current is drawing from its environment (see note 29). In the Lorenz route to chaos, as this energy consumption increases, the complexity of the dynamics of the Lorenz system (and the convection current it models) also increase, culminating in the emergence of the Lorenz attractor. This phenomenon harmonizes very well with the hypothesis that there is a relationship between a society's capacity to harness the energy resources in its environment and its complexity, as measured by its "forms of organization and control" (Baker, 1993:125-6, provides a synopsis of this hypothesis and its long history).
Complexity itself has recently been hailed as an "emerging science at the edge of order and chaos" (Waldrop, 1992:title). Complexity, in this sense, is the study of complex systems taken from fields such as biology and economics.[34] What characterizes a complex system is that it consists of "a great many independent agents ... interacting with each other in a great many ways" (Waldrop, 1992:11). Complexity theory is virtually a subset of chaos theory as we have defined it.[35] However, a complex system may correspond to a dynamical system with thousands or billions of dimensions, and typically chaos theory focuses on lower-dimensional systems as we have in this paper. Wolfram (1984) suggests that, in principle, any material process can be simulated by a dynamical system of sufficient complexity.[36]
One of the most interesting observations of complexity theorists is that complex systems often exhibit spontaneous self-organization (Waldrop, 1992:11) whereby their dynamics become increasingly complex in a kind of evolution towards a thin edge between predictable order and total randomness, an edge that is sometimes termed the edge of chaos (Waldrop, 1992:230). Furthermore, the dynamics of both living processes and socioeconomic interactions seem to evolve towards this edge.[37] These ideas indicate that social systems are almost organic--lifelike--and that they may structure themselves spontaneously in a process akin to biological evolution. The Lorenz route to chaos, symbolizing for us the emergence of social unidiversity from social uniformity in a Bahá'í community, is reminiscent of this lifelike process of spontaneous self-organization.[38]
Bahá'ís see the history of humanity as being essentially progressive and evolutionary, although frequently marked by setbacks and difficulties as well (Cf. Lerche, 1994). Moreover, Bahá'ís view unidiversity as something desirable not only in their own local communities, but in the world community as well. To Bahá'ís, unidiversity at the global level represents something almost organic, something akin to a living being (Universal House of Justice, 1986: 2-3). The advancement of humankind is something Bahá'ís hope to promote by encouraging this kind of global unidiversity.[39]
The global village can be regarded as an immense complex system whose interacting agents are people, cultures, nations, and trading blocs. Due to the nature of nonlinear dynamics, it is not at all predictable what effects Bahá'ís, or any other group, can have on the global system. However, it is possible for a small disturbance to have a large impact on a dynamical system, if that system is in an unstable state. Perhaps it is also possible for participants in the global village to move the world we all share to a new, unidiverse, attractor.
This paper has hopefully convinced its audience that chaos theory is a useful tool for expressing metaphorically a particular viewpoint on certain features of social processes. The authors believe, moreover, that chaos theory is also valuable for expressing other philosophical perspectives on social processes. In the presentation of our metaphors, we have conducted something of a tour of most of the important ideas related to chaotic dynamics. It is our hope that other social researchers will find this information to be of value.
[1] We use the term "dynamical" since the mathematical and scientific literature on chaos theory invariably uses the term "dynamical systems" to describe the kinds of equations we use in our paper.
[2] Nevertheless, qualitative aspects of the dynamical systems presented here seem to be common in many natural phenomena, such as the development of a convection current in the Earth's atmosphere (Lorenz, 1963; Gleick 1987:11-31). Moreover, even some quantitative features of chaotic dynamics are universal to broad classes of dynamical systems. For example, Feigenbaum (1978) has shown that a large class of dynamical systems have period-doubling behavior that is quantitatively identical in some ways. Surprisingly, similar period-doubling behavior has been observed in the fluid turbulence experiments of Libchaber (Gleick, 1987:205) and the dripping faucet investigations of Robert Shaw (Gleick, 1987:265).
Some fundamental qualitative features of dynamical systems have also been observed in social phenomena. For instance, Carneiro's (1987) research indicates that something like a pitchfork bifurcation (discussed elsewhere in this paper) occurs in the development of autonomous villages: at a certain critical size--roughly 2000 people, growing autonomous villages either split into smaller such villages or become part of larger political structures (in which case, they lose some of their autonomy). Despite the fact that the interacting elements of the natural sciences (e.g., quarks, molecules, cells) are very different from those of the social sciences (e.g., people, cultures, economies), the work of Carneiro suggests that some common qualitative dynamical characteristics of the natural world may be ubiquitous in the social realm as well.
[3] A useful introduction to the history and teachings of the Bahá'í Faith is Hatcher and Martin (1985).
[4] The "Bahá'í Faith" is the proper designation of this religion, although there are a number of other designations, depending on the author's or researcher's intent. For example, the term "Bahá'í religion" is acceptable if it implies a scholarly study; "Bahá'í community" is for studies with a sociological focus. "Bahá'ísm" is widely used, but Bahá'ís see the term as pejorative. "Bahá'í" without the noun (as in "the spread of the Bahá'í") irritates Bahá'ís, because it makes linguistic nonsense (equivalent to saying "the spread of the Buddhist"). Very few use "Bahá'í cult" nowawdays except in the case of some religious critics.
[5] Van den Hoonaard (1996) offers a detailed historical and sociological analysis of the establishment of the Bahá'í Community of Canada as a transplantation of a non-Western movement in a Western setting.
[6] For example, a driven pendulum and certain magnetic oscillators can exhibit unpredictable, chaotic dynamics (Gleick, 1987:42-43). Even our solar system, one of the icons of classical mechanics, can behave chaotically in some regions such as the asteroid belt between the planets Mars and Jupiter (Briggs and Peat, 1989:41-43).
[7] Prigogine and Stengers (1984:131-153) describe the chaotic behavior of certain chemical reactions such as the Belousov-Zhabotinsky reaction. Gleick (1987:275-300) reports on the chaotic dynamics of some biological phenomena, specific pathologies of eye movement and cardiac rhythms for example.
[8] The term originated from the title of a paper by Li and Yorke (1975) in which a class of one-dimensional dynamical systems was studied.
[9] Patterns and order can be seen in all of the examples cited in the notes above. The logistic equation, used in biology to model the dynamics of the size of a population with a limited food supply, provides one of the most stunning illustrations of patterns in chaotic dynamics: depending on the birthrate, the size of the population can exhibit a remarkable collection of periodic and aperiodic behaviors (see note 15). Robert May (1974) was the first to notice the extraordinary dynamics of the logistic equation. Gleick (1987:59-80) gives an engaging account of this equation including a graphical depiction of its behavior.
[10] The most serious flaw in Young's papers is an overall presentation of nonlinear dynamics that frequently is superficial, often is obscure, and occasionally is fundamentally erroneous. His descriptions of such concepts as attractor, stability, and bifurcation are sometimes wonderfully poetic, but their clarity and accuracy are enough at times to make a mathematician (one of the authors, for instance) wince. Young writes, for example, "the study of phase-space of a business might be confined to some few attractors; say profit, growth and market share, each with three dimensions of magnitude, duration and periodicity" (1991a:332). Profit and market share are variables, not attractors; since growth is simply a change in one or more variables, an independent variable is not needed to describe it. Independent dimensions (variables) are certainly not needed to describe magnitude, duration and periodicity. These quantities can be determined directly from the dynamics of the variables. Hence, in Young's business example, there are really only two independent variables, profit and market share, and these correspond to two dimensions in phase space. An attractor in this case embodies the long-term behavior of both variables for some set of initial values.
Young makes some dangerous errors regarding the role of period-doubling bifurcations (see note 15) in social processes. He writes, for example, "when land holdings bifurcate such that the average holdings of one group are doubled four times, i.e., are 16 or more times as large as the land holdings of a second group, one can expect destabilizing chaos" (1991b:296). First, this remark demonstrates that Young has confused the doubling of a parameter (in this case, the ratio of one group's land holdings to those of another) related to the dynamical system with the doubling of a period (i.e., the time required for a variable evolving in a periodic way to return to a previous state). Secondly, this remark reveals a confusion between the period-doubling route to chaos and the Ruelle-Takens route (see note 32).
[11] Ann Boyles (1994) gives an accounting of the Bahá'í position on postmodernism.
[12] The authors, as adherents to the Bahá'í Faith, have made a deliberate decision to write this article from a Bahá'í perspective. We emphasize that the views expressed in this paper are those of the authors alone and in no way represent an official Bahá'í position.
[13] The pitchfork bifurcation equation can be written as
[14] In general, a fixed point can be an attractor, a repeller, or neither. A fixed point is said to be stable if a solution whose initial value is close to the fixed point remains close to the fixed point for all future times. Hence, a fixed point attractor is stable (and a fixed point repeller is unstable), but a stable fixed point might not be an attractor.
[15] Besides the pitchfork bifurcation, two other bifurcation types that are noteworthy in the context of this paper are the period-doubling bifurcation and the Hopf bifurcation. The logistic equation (May, 1974; Gleick, 1987:59-80), used to model population dynamics in discrete one-year time steps, provides a good example of a sequence of period-doubling bifurcations. When a parameter (the population's birthrate) of the logistic equation is sufficiently small, the equation has a single fixed point attractor. However, as the parameter is increased, a period-doubling bifurcation occurs which replaces the fixed point attractor with a cycle attractor of period two (i.e., the size of the population oscillates between two values in alternate years). As the parameter is increased further, another period-doubling bifurcation occurs which replaces the cycle attractor of period two with a cycle attractor of period four. Subsequent increases in the parameter cause period-doubling bifurcations to occur more and more frequently creating an infinite succession of cycle attractors of periods 8, 16, 32, etc.; eventually, when the parameter is sufficiently large, the logistic equation has unpredictable, chaotic dynamics except for narrow ranges of the parameter where order exists in the form of cycle attractors of various periods.
A Hopf bifurcation (named after scientist Eberhard Hopf) adds an extra dimension (or oscillation) to an attractor existing in a continuous dynamical system. For example, a Hopf bifurcation transforms a (zero-dimensional) fixed point attractor into a (one-dimensional) cycle attractor with a certain period of oscillation; an additional Hopf bifurcation transforms this cycle attractor into a two-dimensional torus attractor (characterized by two simultaneous oscillations with different periods). Briggs and Peat (1989:31-52) offer a very accessible treatment of these ideas.
[16] Note that the curves x = ?p and x = -?p are the top and bottom halves, respectively, of a single parabola whose equation is p = x2.
[17] In Australia, where the Chinese form a small minority, Chinese adolescents consider themselves less Chinese and more Australian; however, in San Francisco, California, where there is a much larger Chinese community, the youth regard themselves more as Chinese than American (Rosenthal and Feldman, 1992: 223).
[18] This term suggests that the larger, wider community is central to one's worldview, as opposed to ethnocentricity.
[19] In higher-dimensional nonlinear dynamical systems, such as those discussed in the next two sections, solutions often wander in an apparently random way for a long time before finally starting to converge to an attractor. Metaphorically, this is suggestive of people who wander aimlessly through life with no apparent direction until they become attracted to some idea, cause, or lifestyle.
[20] In our pitchfork bifurcation model, x varies continuously. The model could be enhanced to better portray the discontinuous effects of some catalyst on a real social system. M. Warburg comments (1993), for example, that the "situation in Bosnia could be seen as an example of a society with high ethnic heterogeneity (i.e. p>0). Before the breakup of Yugoslavia the various ethnic groups appeared to co-exist peacefully, i.e. society was approaching the positive attractor. Now, it is evidently the opposite. The war was an outside factor which could be said to reset x to a new and now negative value, and Bosnian society then rapidly iterated towards this new situation with extreme ethnocentricity."
[21] Lewis and Stevens (1986) have published a concise and well-balanced statement about the cultural differences between Iranian refugees and Americans, suggesting ways to handle such differences in everyday interactions.
[22] For Persian Bahá'ís, the boundaries of the Bahá'í Faith are determined by Bahá'í scripture, while for Western Bahá'ís, the boundaries are primarily fixed by Bahá'í practice (cf. Warburg, 1990: 5 and 9).
[23] In some cities, the Canadian cultural mainstream seems to have remained quite stable; in some others, the influx of Persians was sufficient to establish Persian Bahá'í culture as the new cultural mainstream of Bahá'í collective life (Anon, 1988: 4).
[24] The observation of these holy days always involves some planned community activities and, if possible, refraining from work.
[25] The discrete dynamical system we have chosen is
[26] `Abdu'l-Bahá, oldest son of the Founder of the Bahá'i Faith and the Leader of the faith from 1892 to 1921, used the following image comparing human diversity to that of a garden: "Diversity of color, form and shape enricheth and adorneth the garden, and heighteneth the effect thereof" (cited in Hatcher and Martin, 1985:79).
[27] Bahá'u'lláh, the Founder of the Bahá'í Faith, wrote, for example, that "the well-being of mankind, its peace and security, are unattainable unless and until its unity is firmly established" (Bahá'u'lláh, 1976:286).
[28] This term was used by Shoghi Effendi, the Guardian of the Bahá'í Faith from 1921 to 1957, who wrote, regarding the requisites of the world-wide administrative order outlined by Bahá'u'lláh, that:
It does not ignore, nor does it attempt to suppress, the diversity of ethnical origins, of climate, of history, of language and tradition, of thought and habit, that differentiate the peoples and nations of the world. It calls for a wider loyalty, for a larger aspiration than any that has animated the human race. It insists upon the subordination of national impulses and interests to the imperative claims of a unified world. It repudiates excessive centralization on one hand and disclaims all attempts at uniformity on the other. Its watchword is unity in diversity (Shoghi Effendi, 1974:41-42).
[29] The Lorenz system, developed by meteorologist
Edward Lorenz (1963) to model a convection current between the warm surface of
the Earth and a cold air mass above, is a continuous dynamical system
comprising the three equations
[30] Phase space here is represented by plotting the three variables x, y, and z on mutually perpendicular axes. For visual clarity, these axes are not shown in figure 3. Note also that, since a page is only two-dimensional, the three-dimensional nature of this figure must be imagined somewhat.
[31] The Bahá'í Iranian refugees in Canada settled in over 90 towns across Canada (Bahá'í Canada, Jan-Feb. 1983: 33). Both Saint-Blancat (1989:32) and Bozorgmehr (1992) suggest more intensive contact of Iranian Bahá'ís with the larger Italian and Los Angeles population, respectively, than is the case of other Iranian groups, such as Shi'áh.
[32] There are a number of well-established routes, involving a sequence of bifurcations, from an equilibrium state (or, equivalently, a fixed point attractor) to the kind of full-blown, almost random, chaotic dynamics suggestive of a turbulent fluid flow. The Lorenz route to chaos involves a pitchfork bifurcation, which transforms a fixed point attractor into two competing fixed point attractors, and subsequent bifurcations, which produce the Lorenz attractor. The infinite sequence of period-doubling bifurcations exhibited by the logistic equation (among others) is another route to chaos, known as the period-doubling route (see note 15). Yet another route to chaos, sometimes termed the Ruelle-Takens route (Ruelle and Takens, 1971), consists of three Hopf bifurcations (see note 15) followed by a fourth bifurcation of a different kind. An accessible account of the Ruelle-Takens route is given by Briggs and Peat (1989:45-52). The main focus of Bergé et al (1984) is an examination of various routes to chaos.
[33] The Mandelbrot set, named after mathematician Benoit Mandelbrot who discovered it, is closely related to a certain discrete dynamical system. See Mandelbrot (1983:180-192) or Becker and Dörfler (1989:128-176) for details on its construction.
[34] One example of a complex system is a genetic circuit comprising regulatory genes which switch each other off and on and, in so doing, govern cellular differentiation (Waldrop, 1992:99-135). Another example is an economic system of independent agents, each of whom makes decisions based on a limited set of assumptions or rules (Waldrop, 1992:241-274).
[35] This follows from the fact that the computer simulations used to study complex systems are equivalent to dynamical systems (usually of the nonlinear variety).
[36] Wolfram (1984) expresses this idea in the language of cellular automata, arrays of cells each of which may be in one of several states, which are sometimes used in computer simulations of complex systems. A cellular automaton can be described exactly by a (generally nonlinear) discrete dynamical system with one equation (dimension) per cell. If Wolfram's suggestion is correct, there is a theoretical basis for contending that the simple metaphors used in this paper may capture some features of social reality.
[37] Waldrop (1992:198-240, 292-4) offers an informative treatment of this "edge of chaos" theory, which has its origins in the study of cellular automata by Stephen Wolfram (see note 36) and others. The dynamical behavior of these automata can be partitioned into four universality classes. The first two of these classes describe behavior that is very ordered, the behavior associated with fixed point and cyclic attractors respectively. The third class describes totally random dynamics or chaos. (Note that Waldrop's usage of the term chaos differs somewhat from that of chaos theorists. For the latter, the term denotes apparently random, but subtly ordered, dynamics; for Waldrop, chaos denotes completely random dynamics with no underlying order or patterns.) The fourth class, labelled the edge of chaos or complexity, describes behavior that lies in a narrow band between the second and third classes, behavior that is lifelike in that it is ordered but not always predictable (Waldrop, 1992:225-230).
[38] There is one important difference, however. The Lorenz route to chaos is not spontaneous; it requires an external agency to increase the parameter R.
[39] Ervin Laszlo, in a foreword to a Bahá'í statement on peace, has also expressed this hope in the language of dynamical systems:
If a group of people in possession of the ideas and the faith of the Bahá'í act in concert and with conscious knowledge of the dynamics of the historical juncture in which humanity now finds itself, they can decisively influence and change the present course of history. In the language of the new sciences of evolution, they can be the small, initially peripheral fluctuation which can be suddenly amplified in a complex dynamical system when that system becomes critically unstable, and which, amplified and spreading, can determine the course of the coming bifurcation (Laszlo, 1986:xiv).
BAHA'I INTERNATIONAL COMMUNITY. Statement to the 37th Session of the
Sub-Commission on Prevention of Discrimination and Protection of Minorities.
Agenda Item 11. Geneva. August 1984 . 4pp.
BAHA'U'LLAH. Gleanings from the Writings of Bahá'u'lláh.
2nd Ed. Translated by
Shoghi Effendi. Wilmette, IL: Bahá'í Publishing Trust. 1976.
BAKER, P. L. Chaos, order, and sociological theory. Sociological Inquiry
1993, 63 (2), 123-149.
---- Letter to W.C. van den Hoonaard, 17 February 1994.
BARBER, B. R. Jihad vs. McWorld. The Atlantic Monthly. 1992, 269
(3), 53-63.
BECKER, K.-H. & DORFLER, M. Dynamical systems and fractals: Computer
graphics experiments in Pascal. Cambridge: Cambridge University Press.
1989.
BERGE, P., POMEAU, Y. & VIDAL, C. Order within chaos: Towards a deterministic approach to turbulence. New York: John Wiley & Sons.
1986.
BLAU, P. M. Inequality and heterogeneity: A primitive theory of social
structure.
New York. Free Press. 1977.
BOYLES, A. World Watch. The Bahá'í World, 1993-1994.
Oxford: World Centre
Publications, 171-188.
BOZORGMEHR, M. Internal ethnicity: Armenian, Bahá'í, Jewish, and Muslim
Iranians in Los Angeles. Ph.D. Dissertation. Department of Sociology,
University of California, Los Angeles. 1992.
BRIGGS, J. & PEAT, F.D. Turbulent mirror: An illustrated guide to chaos
theory and the science of wholeness. New York: Harper & Row. 1989.
CARNEIRO, R. L. The Evolution of complexity in human societies and its
mathematical expression. International Journal of Comparative Sociology.
1987, 28 (3-4), 111-127.
DANESH, H. The challenge of integration, Part I. Bahá'í
Canada, Oct. 1986a, 8 (8).
---- The challenge of integration, Part II. Bahá'í Canada.
Nov. 1986b, 8 (9).
---- The challenge of integration, Part III. Bahá'í
Canada. Dec. 1986c, 8 (10).
---- Three stages of integration: Part II. Bahá'í Canada.
Jan. 1988, 9 (11), 15-17.
FEATHER, N.T., VOLKMER, V.E., & McKee, I.R. A Comparative study of the
value priorities of Australians, Australian Bahá'ís, and
Expatriate Iranian Bahá'ís. Journal of Cross-Cultural
Psychology. 1992, 1, 96-106.
FEIGENBAUM, M. Quantitative universality for a class of nonlinear
transformations. Journal of Statistical Physics. 1978, 19,
25-52.
GLEICK, J. Chaos: making a new science. New York: Viking. 1987.
GREGERSEN, H., & SAILER, L. Chaos theory and its implications for social
science research. Human Relations. 1993, 46 (7), 777-802.
GUCKENHEIMER, J. & HOLMES, P. Nonlinear oscillations, dynamical
systems, and bifurcations of vector fields. New York: Springer-Verlag. 1983.
HARVEY, D. The Condition of modernity: an enquiry into the origins of
cultural change. Oxford: Oxford University Press. 1989.
HATCHER, W. S. & MARTIN, J.D. The Bahá'í Faith: The
emerging global religion. San Francisco: Harper & Row. 1985.
HOWE, L. Bahá'í Community Life: The Nineteen-Day Feast.
Undergraduate Essay on
Culture as Performance, York University, Toronto. 1988.
LASZLO, E. The foreword, pp. xiii-xiv, of To the peoples of the world:
A Bahá'í statement on peace by the Universal House of
Justice. Edited by Hossain Danesh. Ottawa: The Association for
Bahá'í Studies. 1986
LERCHE, C. `Us and them:' A study of alienation and world order. Journal
of Bahá'í Studies. 1994, 5 (4), 17-31.
LEWIS, F. & Stevens, P. Iranian refugees in America: A cross-cultural
perspective.
Wilmette, Ill. United States Bahá'í Refugee Office. 1986
LI, T.Y. & YORKE, J.A. Period three implies chaos. American
Mathematical Monthly. 1975, 82, 985-992.
LORENZ, E.N. Deterministic non-periodic flow. Journal of the
Atmospheric Sciences. 1963, 20, 130-141.
MACEOIN, D. Emerging from Obscurity?: Recent Developments in Bahá'ísm.
Religion Today: A Journal of Contemporary Religions. 1986, 3 (1),
1-5.
---- A people apart: The Bahá'í community of Iran in the
twentieth century. Centre of
Near and Middle Eastern Studies, University of London. Occasional Paper 4.
1989.
MANDELBROT, B. B. The fractal geometry of nature. New York: W.H.
Freeman
and Company. 1983.
MAY, R. Biological populations with nonoverlapping generations, stable
points,
stable cycles, and chaos. Science. 1974, 186, 645-647.
PRIGOGINE, I. & STENGERS, I. Order out of chaos: Man's new
dialogue with nature. Boulder, CO: New Science Library. 1984
RAFAT, P. The beauty and challenge of diversity. Bahá'í
Canada. 1988, 10 (8),
16, 18.
ROSENTHAL, D. A. & FELDMAN, S.S. The nature and stability of ethnic
identity
in Chinese youth. Journal of Cross-Cultural Psychology. 1992, 23
(12), 214-227.
RUELLE, D. & TAKENS, F. On the nature of turbulence. Communications in
Mathematical Physics. 1971, 20, 167-192.
SAINT-BLANCAT, C. Nation et religion chez les immigrés iraniens en
Italie. Arch. Sc. soc. des Religions. 1989, 68 (1), 27-37.
SHOGHI EFFENDI The world order of Bahá'u'lláh, Selected
Letters. 2nd Ed.
Wilmette, IL: Bahá'í Publishing Trust. 1974.
SMART, B. Postmodernity. London: Routledge. 1993.
TOFFLER, A. Future shock. New York: Random House. 1970.
TOURAINE, A. The post-industrial society. London: Wildwood. 1974.
VAN DEN HOONAARD, W.C. The Bahá'ís in Canada: A Study in the
Transplantation of non-Western religious movements to Western societies."
ARC: The Journal of the Faculty of Religious Studies. McGill University.
1996, 24.
WALDROP, M. M. Complexity: The emerging science at the edge of order
and chaos. New York: Simon & Schuster. 1992.
WARBURG, M. Units of analysis and the study of religious minorities. Paper
presented to the International Association for the History of Religions, Rome,
3-8 Sept. 1990.
---- Letter to W.C. van den Hoonaard, Fredericton, New Brunswick. 20 December
1993.
---- Religious Innovation in Denmark: The Establishment and Growth of
the Danish Bahá'í Community, 1925-1987. Bahá'ís
in the West: Studies in Bábí and Bahá'í
History. 6, Los Angeles, CA: Kalimat (forthcoming).
WOLFRAM, S. Computer software in science and mathematics. Scientific
American.
1984, 251 (3), 188-203.
YOUNG, T.R. Chaos theory and symbolic interaction theory: Poetics for the
postmodern sociologist. Symbolic Interaction. 1991a, 14,
321-334.
---- Chaos and social change: Metaphysics of the postmodern. The Social
Science Journal 1991b, 28, 289-305.
|
|